3D для Mobile Basic
от Gifo_Gsoul
Как вы поняли, речь здесь пойдёт не о какой то торговой марке или названии программы, речь пойдет о трёхмерном пространстве (Длина, Ширина, Высота).
3Д само по себе нельзя открыть на двумерном экране монитора вашего компьютера или телефоне, поэтому используются технологии отображения 3Д на 2-мерную плоскость, грубо говоря, выводится лишь проекция. Любые 3Д игры, будь то ГТА5, КРИЗИС3 или КОНТР СТРАЙК, во всех них выводится лишь проекция с определенными надстроенными параметрами. Сегодня я расскажу, каким образом вывести подобные проекции.
Как и у любых чуваков-кодеров у меня возникло желание делать 3д-игру на телефон, под рукой был mobile basic и дело попахивало извращенством. Поэтому я решил сам вывести формулу отображения 3д проекции, к тому времени я еще не догадывался гуглить, просто своё приятней
Итак, что главное в отображение 3д?!
Если вы поднимите первую руку и поднесете её прямо непосредственно к носу, а вторую расположите вдали, то при перемещении их на одинаковое расстояние вы заметите: дальние объекты по проекции двигаются медленней ближних!
Это самое главное правило, при составлении 3Д формулы.
Перейдём к следующему этапу.
В обычной 2-мерной плоскости "х-у" _ координата z=0 - и это константа.
Написав X=X+1 - перемещение Х происходит ровно на 1.
В 3Д пространстве проекция же точки могла бы перемещаться визуально быстрее или медленнее чем на 1.
Поэтому немного изменим запись для проекции 3Д: Х=Х+1*f(z).
f(z)- функция, зависящая от зет. Давайте начнём её выводить:
При Z=0 -> f(z)=1. Единицу можно представить как отношение между собой двух одинаковых чисел/переменных. Пусть пока будет так: f(z)=a/a.
Вспомнив основное правило отображения 3д (чем дальше объект, тем визуально медленней он движется) можно догадаться, что подобная закономерность выражается в дроби (1/z) - чем больше зет, тем меньше значение дроби и на меньшее расстояние переносит координату. В функции f(z) мы уже задали дробь и будем дальше её усовершенствовать.
Итак, ЗЕТ находится в знаменателе, следовательно это либо (a/a*z) либо (a/a+z).
Учитывая, что при Z=0 -> f(z)=1, то f(z)=(a/a+z), где а - параметр, который может являться любым числом, на своё усмотрение я выбрал а=16, его корректировка изменяет характеристики отображения 3Д.
Но, не стоит расслабляться, после применения подобной формулы отображение 3Д было очень резким и растянутым, видимо значение ЗЕТ в знаменателе было достаточно большим, поэтому его нужно насильно уменьшить, умножив его на маленькое число-коэффициент, которое изменяется от 0 до 1.
Получаем следующее: f(z)=(a/a+z*kof), где kof - число от 0 до 1, я для себя выбрал лично 0.05. Таким образом у меня вышло так: f(z)=(16/(16+0.05*z)). Вы можете подобрать другие параметры 'a' и 'kof' на своё усмотрение.
Вывод проекции на экран.
Функция f(z) готова. Напомню, что мы пытаемся вывести проекцию 3д точки на 2д плоскость, т.е. в 2д координатах.
Пусть 3д точка: x_3d, y_3d, z_3d
Проекция 3д точки на 2д плоскость: x_2d, y_2d
Тогда:
x_2d = x_3d * (16 / (16 + 0.05 * z_3d))
y_2d = y_3d * (16 / (16 + 0.05 * z_3d))
Но для нашего воображения проще будет задавать координаты от центра экрана и так, как показано на (рисунке 1).
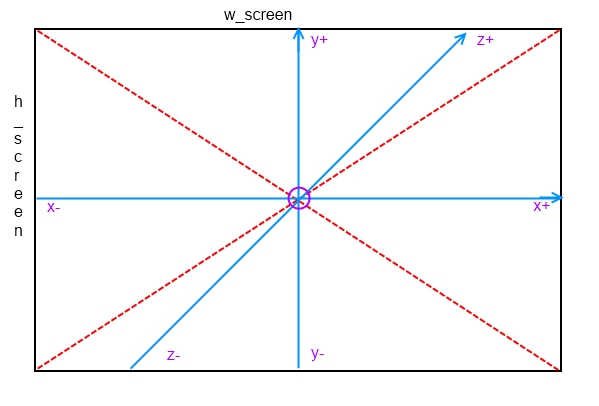Рисунок - 1. Позиционирование осей [x, y, z] относительно экрана.
x_2d = (wscreen / 2) + x_3d * (16 / (16 + 0.05 * z_3d))
y_2d = (hscreen / 2) - y_3d * (16 / (16 + 0.05 * z_3d))
wscreen, hscreen - ширина и высота экрана соответственно.
Как вы ещё заметили, в формуле 'y_2d' после (hscreen / 2) стоит знак минус, это потому, чтобы инвертировать направление изменения оси 'игрик', так как на экране монитора 'игрик' увеличивается направлением вниз, а в привычном нам математическом представлении 'игрик' увеличивается направлением вверх.
Вот в принципе и всё, формула 3Д отображения готова!
А вот и долгожданная практика!
Теперь начнём на практике, попробуем составить код на mobile basic для отображения куба
Запишем реальные 3д координаты нашего куба:
Что то меня занесло и я написал целый код по отображению. Ну да ладно.
Что же делает этот код? Он рисует куб и даёт вам возможность его перемещать по:
Оси X - кнопки 4 и 6
Оси Y - кнопки 2 и 8
Оси Z - кнопки 1 и 3
Можно так же реализовать вращение по осям, для это вам потребуется параметрическая запись уравнения окружности:
X=x0+R*COS(alf)
Y=y0+R*SIN(alf)
Где x0 и y0 - координаты центра окружности
R - радиус
alf - угол, на котором появится точка на окружности.
Можно так же реализовать и заливку граней, примитивами (fillrect, fillarc, drawline и т.д.)
Можно реализовать и достаточно примитивное освещение в зависимости от дальности (как я сделал в своей игре Sonic Time 3D)
Но это уже - "Думайте сами, решайте сами" (Высоцкий)
P.S. Я конечно могу еще запилить свои файлы - моельки 3д и поддержку их в mobile basic, даже программку для их редактирования на компьютере, но это только, если будет достаточно много желающих.
А на последок я выкладываю ссылку на видеоролик по "краткому обзору без слов" моей игры:
"Sonic Time 3D"
3Д само по себе нельзя открыть на двумерном экране монитора вашего компьютера или телефоне, поэтому используются технологии отображения 3Д на 2-мерную плоскость, грубо говоря, выводится лишь проекция. Любые 3Д игры, будь то ГТА5, КРИЗИС3 или КОНТР СТРАЙК, во всех них выводится лишь проекция с определенными надстроенными параметрами. Сегодня я расскажу, каким образом вывести подобные проекции.
Как и у любых чуваков-кодеров у меня возникло желание делать 3д-игру на телефон, под рукой был mobile basic и дело попахивало извращенством. Поэтому я решил сам вывести формулу отображения 3д проекции, к тому времени я еще не догадывался гуглить, просто своё приятней
Итак, что главное в отображение 3д?!
Если вы поднимите первую руку и поднесете её прямо непосредственно к носу, а вторую расположите вдали, то при перемещении их на одинаковое расстояние вы заметите: дальние объекты по проекции двигаются медленней ближних!
Это самое главное правило, при составлении 3Д формулы.
Перейдём к следующему этапу.
В обычной 2-мерной плоскости "х-у" _ координата z=0 - и это константа.
Написав X=X+1 - перемещение Х происходит ровно на 1.
В 3Д пространстве проекция же точки могла бы перемещаться визуально быстрее или медленнее чем на 1.
Поэтому немного изменим запись для проекции 3Д: Х=Х+1*f(z).
f(z)- функция, зависящая от зет. Давайте начнём её выводить:
При Z=0 -> f(z)=1. Единицу можно представить как отношение между собой двух одинаковых чисел/переменных. Пусть пока будет так: f(z)=a/a.
Вспомнив основное правило отображения 3д (чем дальше объект, тем визуально медленней он движется) можно догадаться, что подобная закономерность выражается в дроби (1/z) - чем больше зет, тем меньше значение дроби и на меньшее расстояние переносит координату. В функции f(z) мы уже задали дробь и будем дальше её усовершенствовать.
Итак, ЗЕТ находится в знаменателе, следовательно это либо (a/a*z) либо (a/a+z).
Учитывая, что при Z=0 -> f(z)=1, то f(z)=(a/a+z), где а - параметр, который может являться любым числом, на своё усмотрение я выбрал а=16, его корректировка изменяет характеристики отображения 3Д.
Но, не стоит расслабляться, после применения подобной формулы отображение 3Д было очень резким и растянутым, видимо значение ЗЕТ в знаменателе было достаточно большим, поэтому его нужно насильно уменьшить, умножив его на маленькое число-коэффициент, которое изменяется от 0 до 1.
Получаем следующее: f(z)=(a/a+z*kof), где kof - число от 0 до 1, я для себя выбрал лично 0.05. Таким образом у меня вышло так: f(z)=(16/(16+0.05*z)). Вы можете подобрать другие параметры 'a' и 'kof' на своё усмотрение.
Вывод проекции на экран.
Функция f(z) готова. Напомню, что мы пытаемся вывести проекцию 3д точки на 2д плоскость, т.е. в 2д координатах.
Пусть 3д точка: x_3d, y_3d, z_3d
Проекция 3д точки на 2д плоскость: x_2d, y_2d
Тогда:
x_2d = x_3d * (16 / (16 + 0.05 * z_3d))
y_2d = y_3d * (16 / (16 + 0.05 * z_3d))
Но для нашего воображения проще будет задавать координаты от центра экрана и так, как показано на (рисунке 1).
Рисунок - 1. Позиционирование осей [x, y, z] относительно экрана.x_2d = (wscreen / 2) + x_3d * (16 / (16 + 0.05 * z_3d))
y_2d = (hscreen / 2) - y_3d * (16 / (16 + 0.05 * z_3d))
wscreen, hscreen - ширина и высота экрана соответственно.
Как вы ещё заметили, в формуле 'y_2d' после (hscreen / 2) стоит знак минус, это потому, чтобы инвертировать направление изменения оси 'игрик', так как на экране монитора 'игрик' увеличивается направлением вниз, а в привычном нам математическом представлении 'игрик' увеличивается направлением вверх.
Вот в принципе и всё, формула 3Д отображения готова!
А вот и долгожданная практика!
Теперь начнём на практике, попробуем составить код на mobile basic для отображения куба
Запишем реальные 3д координаты нашего куба:
- 10 wscreen=screenwidth(0):hscreen=screenheight(0)
- 15 n%=8
- 16 DIM x_3d(n%): DIM y_3d(n%): DIM z_3d(n%)
- 17 DIM x_2d(n%): DIM y_2d(n%)
- 20 x_3d(0)=-50:y_3d(0)=50:z_3d(0)=150
- 21 x_3d(1)=50:y_3d(1)=50:z_3d(1)=150
- 22 x_3d(2)=50:y_3d(2)=50:z_3d(2)=50
- 23 x_3d(3)=-50:y_3d(3)=50:z_3d(3)=50
- 24 x_3d(4)=-50:y_3d(4)=-50:z_3d(4)=150
- 25 x_3d(5)=50:y_3d(5)=-50:z_3d(5)=150
- 26 x_3d(6)=50:y_3d(6)=-50:z_3d(6)=50
- 27 x_3d(7)=-50:y_3d(7)=-50:z_3d(7)=50
- 30 for t%=0 to n%-1
- 31 x_2d(t%)=(wscreen/2)+x_3d(t%)*(16/(16+0.05*z_3d(t%)))
- 32 y_2d(t%)=(hscreen/2)-y_3d(t%)*(16/(16+0.05*z_3d(t%)))
- 33 next t%
- 35 cls
- 40 drawline x_2d(0),y_2d(0),x_2d(1),y_2d(1)
- 41 drawline x_2d(1),y_2d(1),x_2d(2),y_2d(2)
- 42 drawline x_2d(2),y_2d(2),x_2d(3),y_2d(3)
- 43 drawline x_2d(3),y_2d(3),x_2d(0),y_2d(0)
- 44 drawline x_2d(4),y_2d(4),x_2d(5),y_2d(5)
- 45 drawline x_2d(5),y_2d(5),x_2d(6),y_2d(6)
- 46 drawline x_2d(6),y_2d(6),x_2d(7),y_2d(7)
- 47 drawline x_2d(7),y_2d(7),x_2d(4),y_2d(4)
- 48 drawline x_2d(0),y_2d(0),x_2d(4),y_2d(4)
- 49 drawline x_2d(1),y_2d(1),x_2d(5),y_2d(5)
- 50 drawline x_2d(2),y_2d(2),x_2d(6),y_2d(6)
- 51 drawline x_2d(3),y_2d(3),x_2d(7),y_2d(7)
- 60 repaint
- 70 if left(0) then goto 100
- 71 if right(0) then goto 200
- 72 if up(0) then goto 300
- 73 if down(0) then goto 400
- 74 if gamea(0) then goto 500
- 75 if gameb(0) then goto 600
- 76 goto 30
- 100 for t%=0 to n%-1
- 101 x_3d(t%)=x_3d(t%)-1.5
- 102 next t%
- 103 goto 30
- 200 for t%=0 to n%-1
- 201 x_3d(t%)=x_3d(t%)+1.5
- 202 next t%
- 203 goto 30
- 300 for t%=0 to n%-1
- 301 y_3d(t%)=y_3d(t%)+1.5
- 302 next t%
- 303 goto 30
- 400 for t%=0 to n%-1
- 401 y_3d(t%)=y_3d(t%)-1.5
- 402 next t%
- 403 goto 30
- 500 for t%=0 to n%-1
- 501 z_3d(t%)=z_3d(t%)+1.5
- 502 next t%
- 503 goto 30
- 600 for t%=0 to n%-1
- 601 z_3d(t%)=z_3d(t%)-1.5
- 602 next t%
- 603 goto 30
Что то меня занесло и я написал целый код по отображению. Ну да ладно.
Что же делает этот код? Он рисует куб и даёт вам возможность его перемещать по:
Оси X - кнопки 4 и 6
Оси Y - кнопки 2 и 8
Оси Z - кнопки 1 и 3
Можно так же реализовать вращение по осям, для это вам потребуется параметрическая запись уравнения окружности:
X=x0+R*COS(alf)
Y=y0+R*SIN(alf)
Где x0 и y0 - координаты центра окружности
R - радиус
alf - угол, на котором появится точка на окружности.
Можно так же реализовать и заливку граней, примитивами (fillrect, fillarc, drawline и т.д.)
Можно реализовать и достаточно примитивное освещение в зависимости от дальности (как я сделал в своей игре Sonic Time 3D)
Но это уже - "Думайте сами, решайте сами" (Высоцкий)
P.S. Я конечно могу еще запилить свои файлы - моельки 3д и поддержку их в mobile basic, даже программку для их редактирования на компьютере, но это только, если будет достаточно много желающих.
А на последок я выкладываю ссылку на видеоролик по "краткому обзору без слов" моей игры:
"Sonic Time 3D"
