Я люблю окружности
от aNNiMON
Недавно был поднят вопрос, а зачем, собственно, программисту математика? Хочу поделиться своими мыслями на эту тему, а также рассказать, что именно пригодилось из школьного и университетского курса.
Нас учат неправильно
Прежде всего хотелось бы затронуть тему подачи материала в учебных заведениях. Думаю, у многих нелюбовь (а то и вовсе ненависть) к математике (да и не только к ней) зародилась именно в школьные годы. Если учитель приходит, рассказывает материал, проверяет домашнее задание и задаёт новое, после чего уходит, какая любовь к предмету может появиться?
Так было и со мной. Нам давали материал, мы решали задачки, выходили к доске. Ненависти не было, просто было безразличие и некоторая цель — выйти к доске, чтобы получить хорошую оценку; быстро сделать домашнее задание, чтобы пойти гулять. Так надо, вот и всё. Разумеется, с годами нагрузка возрастала, появлялись другие предметы, сама математика усложнялась да и гулять всё больше хотелось. Безразличие перерастало в отвращение...
Но однажды, наша учительница по алгебре и геометрии заболела и на замену поставили другую — учительницу биологии, которая когда-то давно тоже читала математику. Урок геометрии она начала с истории:
В далёкие времена, когда стремительно развивалось мореходство, перед людьми предстала задача определить, через сколько времени корабль, появившийся на горизонте, прибудет в порт. Скорость кораблей была примерно известна, так что оставалось лишь найти расстояние. Но как это сделать? Не расставлять же прямо в море буйки на каждом километре?
Однако, способ был. На берегу, на уровне следования корабля ставили отметку, затем отмеряли некоторое расстояние от неё вправо или влево и тоже ставили отметку. Получалось три точки: две на берегу и одна — корабль — в море. Что это, как не прямоугольный треугольник?
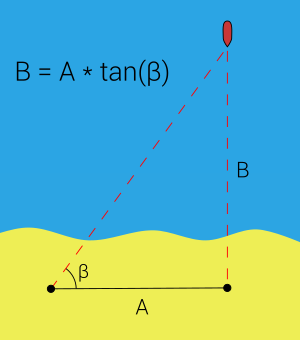
Оставалось только измерить угол на второй отметке и по свойству прямоугольного треугольника расчитать расстояние одного из катетов.
Прошло уже больше десяти лет с того урока, но я всё ещё его помню в деталях. Нам не только рассказали теорию, но и показали, где её можно применить на практике. В результате всё отлично запомнилось и появился интерес к предмету.
Что нужно знать программисту?
Программисту нужно знать всё. Всё, но с некоторой оговорочкой. Ему нужно знать биологию, если он разрабатывает ПО, связанное с этой сферой. Ему нужно знать бухгалтерию, если потребуется автоматизировать составление проводок. Нужно знать и статистику, и астрономию, и географию, и математику, и физику, и анатомию и много чего ещё. Но оговорочка заключается в том, что это всё нужно знать лишь по требованию. Если ты создаёшь сайты, тебе не понадобится биология, бухгалтерия и астрономия, но зато может потребоваться дизайн и психология. Поняли, к чему я веду? Всё, что нужно для работы можно освоить уже потом. Дизайну, например, не учат в школе, да и программистам редко его читают в вузах, но знать нужно будет, если возникнет такая задача. С биологией, физикой, статистикой, астрономией, географией и прочим дела обстоят так же.
Так что нельзя точно ответить на вопросы: нужна ли программисту математика и что нужно знать программисту. Всё зависит от той области, с которой вы будете работать.
Лично я бы советовал слегка подучивать математику, на случай, если всё-таки придётся с ней работать, а уж если действительно припечёт, тогда уже направить все силы на её изучение. Если же она нужна лишь изредка, то статей на Википедии или прочтения нужного раздела в книге должно хватить.
Сэкономленное же время можно потратить на изучение того, что действительно вас интересует, на общение со сверстниками, уделить время родным и близким в конце концов.
Пропорции и окружности
Наконец, о самой теме статьи. Что из математики встречается чаще всего, во всяком случае у меня, что следовало бы знать. Опять же, всё зависит от сферы деятельности, кому-то потребуется знать намного больше, а кому-то и половины описанного хватит.
Самое распространённое это пропорции. Умение составлять пропорции помогает быстро решить множество задач, простых и не очень.
Курс доллара 26.5097 UAH, сколько будет 24.80 USD?
Если боковая панель у окна 800x450 имеет ширину 300 пикселей, то с каким коэффициентом нужно её масштабировать, чтобы и на 1280x720 смотрелось нормально?
либо
Если за 10 секунд скачивается 820 килобайт, размер файла 2.8 Мб, а скачалось уже 1.1 Мб, сколько примерно потребуется времени до окончания загрузки?
На втором месте векторы и матрицы. Скалярное произведение векторов, определитель матрицы, умножение матриц, транспонирование, всё это пригодится, особенно в геймдеве и в графике.
Например, у нас есть графические объекты, скажем, линии, треугольники, квадраты. И есть вот такие матрицы преобразований в 2D плоскости:
Перемещение
Масштабирование
Поворот
Наклон по горизонтали
Наклон по вертикали
Реализовав применение матричных преобразований к каждой точке, открывается сразу куча возможностей - объекты теперь можно перемещать, масштабировать, отражать, наклонять, искажать в перспективе и прочее.
Вот тут поэффектнее на картинках: http://jsfiddle.net/user/rjw57/fiddles/
А если вы ещё не читали статью Линейная алгебра для разработчиков игр / Хабрахабр, самое время это сделать.
На третьем месте по важности у меня окружность, число Пи, а также синусы и косинусы.
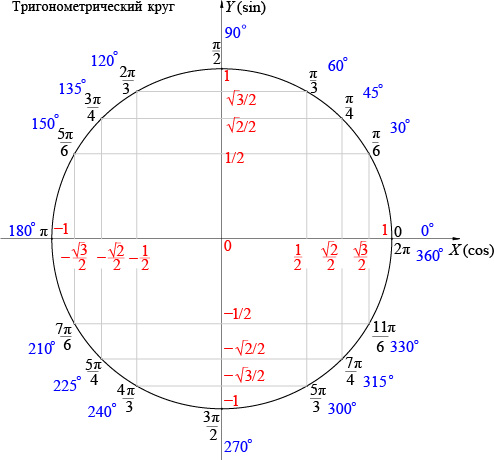
Поняв однажды свойства синуса и косинуса, открылся большой простор для экспериментов.
Самое простое применение синуса и косинуса - рисование многоугольников.
Движение по окружности
Преследование цели тоже использует синус и косинус.
Даже обход препятствий я когда-то делал по окружности в одной из лабораторных, где нужно было создать игру.
Или вот, по текущему времени и времени восхода и заката солнца выбрать соответствующий фон.
Зачем тогда учить сложные разделы математики?
Однажды мы спросили у преподавателя высшей математики, зачем мы учим все эти сложные темы, мучаемся с интегралами, запоминаем жуткие формулы. Он долго уходил от ответа, но в конце концов сказал: а это чтоб вы знали, что такое вообще существует и при необходимости могли применить.
Жаль, что при этом не говорят, где именно тот или иной раздел можно применить на практике, потому что до сих пор бо́льшая часть материала просто висит в теоретическом воздухе, не закреплённая за чем-то конкретным.
Думаю, мой посыл вы поняли, математика нужна, но не в тех объёмах, которыми пичкают неокрепшие умы. И если у вас туго с ней, это не повод отчаиваться. Главное, знать основы, а всё остальное, если понадобится, можно наверстать. А вместо насильного заучивания формул, лучше погуляйте на улице с друзьями. Формула не обидится.
А как вам пригодилась математика?
Нас учат неправильно
Прежде всего хотелось бы затронуть тему подачи материала в учебных заведениях. Думаю, у многих нелюбовь (а то и вовсе ненависть) к математике (да и не только к ней) зародилась именно в школьные годы. Если учитель приходит, рассказывает материал, проверяет домашнее задание и задаёт новое, после чего уходит, какая любовь к предмету может появиться?
Так было и со мной. Нам давали материал, мы решали задачки, выходили к доске. Ненависти не было, просто было безразличие и некоторая цель — выйти к доске, чтобы получить хорошую оценку; быстро сделать домашнее задание, чтобы пойти гулять. Так надо, вот и всё. Разумеется, с годами нагрузка возрастала, появлялись другие предметы, сама математика усложнялась да и гулять всё больше хотелось. Безразличие перерастало в отвращение...
Но однажды, наша учительница по алгебре и геометрии заболела и на замену поставили другую — учительницу биологии, которая когда-то давно тоже читала математику. Урок геометрии она начала с истории:
В далёкие времена, когда стремительно развивалось мореходство, перед людьми предстала задача определить, через сколько времени корабль, появившийся на горизонте, прибудет в порт. Скорость кораблей была примерно известна, так что оставалось лишь найти расстояние. Но как это сделать? Не расставлять же прямо в море буйки на каждом километре?
Однако, способ был. На берегу, на уровне следования корабля ставили отметку, затем отмеряли некоторое расстояние от неё вправо или влево и тоже ставили отметку. Получалось три точки: две на берегу и одна — корабль — в море. Что это, как не прямоугольный треугольник?
Оставалось только измерить угол на второй отметке и по свойству прямоугольного треугольника расчитать расстояние одного из катетов.
Прошло уже больше десяти лет с того урока, но я всё ещё его помню в деталях. Нам не только рассказали теорию, но и показали, где её можно применить на практике. В результате всё отлично запомнилось и появился интерес к предмету.
Что нужно знать программисту?
Программисту нужно знать всё. Всё, но с некоторой оговорочкой. Ему нужно знать биологию, если он разрабатывает ПО, связанное с этой сферой. Ему нужно знать бухгалтерию, если потребуется автоматизировать составление проводок. Нужно знать и статистику, и астрономию, и географию, и математику, и физику, и анатомию и много чего ещё. Но оговорочка заключается в том, что это всё нужно знать лишь по требованию. Если ты создаёшь сайты, тебе не понадобится биология, бухгалтерия и астрономия, но зато может потребоваться дизайн и психология. Поняли, к чему я веду? Всё, что нужно для работы можно освоить уже потом. Дизайну, например, не учат в школе, да и программистам редко его читают в вузах, но знать нужно будет, если возникнет такая задача. С биологией, физикой, статистикой, астрономией, географией и прочим дела обстоят так же.
Так что нельзя точно ответить на вопросы: нужна ли программисту математика и что нужно знать программисту. Всё зависит от той области, с которой вы будете работать.
Лично я бы советовал слегка подучивать математику, на случай, если всё-таки придётся с ней работать, а уж если действительно припечёт, тогда уже направить все силы на её изучение. Если же она нужна лишь изредка, то статей на Википедии или прочтения нужного раздела в книге должно хватить.
Сэкономленное же время можно потратить на изучение того, что действительно вас интересует, на общение со сверстниками, уделить время родным и близким в конце концов.
Пропорции и окружности
Наконец, о самой теме статьи. Что из математики встречается чаще всего, во всяком случае у меня, что следовало бы знать. Опять же, всё зависит от сферы деятельности, кому-то потребуется знать намного больше, а кому-то и половины описанного хватит.
Самое распространённое это пропорции. Умение составлять пропорции помогает быстро решить множество задач, простых и не очень.
Курс доллара 26.5097 UAH, сколько будет 24.80 USD?
- 1 - 26.5097
- 24.80 - x
- x = 24.80 * 26.5097 / 1 = 657.44056 UAH
Если боковая панель у окна 800x450 имеет ширину 300 пикселей, то с каким коэффициентом нужно её масштабировать, чтобы и на 1280x720 смотрелось нормально?
- 800 - 300
- 1280 - x
- x = 1280 * 300 / 800 = 480
- 1280 / 800 = 1.6
- 300 * 1.6 = 480
Если за 10 секунд скачивается 820 килобайт, размер файла 2.8 Мб, а скачалось уже 1.1 Мб, сколько примерно потребуется времени до окончания загрузки?
- 2.8 - 1.1 = 1.7 Мб * 1024 кб = 1740.8 кб осталось скачать
- 820 кб - 10 с
- 1740.8 кб - x с
- x = 1740.8 * 10 / 820 = 21.22 c
На втором месте векторы и матрицы. Скалярное произведение векторов, определитель матрицы, умножение матриц, транспонирование, всё это пригодится, особенно в геймдеве и в графике.
Например, у нас есть графические объекты, скажем, линии, треугольники, квадраты. И есть вот такие матрицы преобразований в 2D плоскости:
Перемещение
Масштабирование
Поворот
Наклон по горизонтали
Наклон по вертикали
Реализовав применение матричных преобразований к каждой точке, открывается сразу куча возможностей - объекты теперь можно перемещать, масштабировать, отражать, наклонять, искажать в перспективе и прочее.
Вот тут поэффектнее на картинках: http://jsfiddle.net/user/rjw57/fiddles/
А если вы ещё не читали статью Линейная алгебра для разработчиков игр / Хабрахабр, самое время это сделать.
На третьем месте по важности у меня окружность, число Пи, а также синусы и косинусы.
Поняв однажды свойства синуса и косинуса, открылся большой простор для экспериментов.
Самое простое применение синуса и косинуса - рисование многоугольников.
- ctx.moveTo(w / 2 + radius, h / 2);
- for (var i = 1; i < nPoints; i++) {
- var a = i * (2 * Math.PI / nPoints);
- ctx.lineTo(w / 2 + Math.cos(a) * radius,
- h / 2 + Math.sin(a) * radius);
- }
- ctx.lineTo(w / 2 + radius, h / 2);
Движение по окружности
Преследование цели тоже использует синус и косинус.
Даже обход препятствий я когда-то делал по окружности в одной из лабораторных, где нужно было создать игру.
Или вот, по текущему времени и времени восхода и заката солнца выбрать соответствующий фон.
Зачем тогда учить сложные разделы математики?
Однажды мы спросили у преподавателя высшей математики, зачем мы учим все эти сложные темы, мучаемся с интегралами, запоминаем жуткие формулы. Он долго уходил от ответа, но в конце концов сказал: а это чтоб вы знали, что такое вообще существует и при необходимости могли применить.
Жаль, что при этом не говорят, где именно тот или иной раздел можно применить на практике, потому что до сих пор бо́льшая часть материала просто висит в теоретическом воздухе, не закреплённая за чем-то конкретным.
Думаю, мой посыл вы поняли, математика нужна, но не в тех объёмах, которыми пичкают неокрепшие умы. И если у вас туго с ней, это не повод отчаиваться. Главное, знать основы, а всё остальное, если понадобится, можно наверстать. А вместо насильного заучивания формул, лучше погуляйте на улице с друзьями. Формула не обидится.
А как вам пригодилась математика?
