Игра «Жизнь» на JavaScript и Python
от M_N
Привет всем!
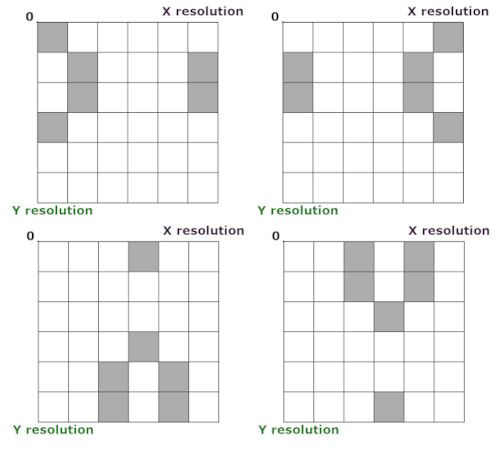
Игра «Жизнь» (Game of Life) придумана Джоном Конвеем в 1970-м году. Это – игра без игроков. Клеточный автомат, имитирующий жизнь колонии неких существ: прямоугольная площадка поделена на клетки, условно их представляющих. Правила просты, но игра интересная. Тут возможны, скажем, такие фигуры:

(нажмите чтобы увидеть анимацию*)Клетка может быть живой или мёртвой. Чем это определяется?
1. Если живую клетку окружает менее 2-х или более 3-х живых соседей, она погибает;
2. Если мёртвую клетку окружает ровно 3 живых соседа, она оживает.
Сделаем свою игру «Жизнь»? Что ж, приступим.
Содержание1. Как работает механика игры
2. Игра «Жизнь» на JavaScript
3. Игра «Жизнь» на Python
Как работает механика игры
Мы должны следовать таким пунктам:
1. Создаём матрицу
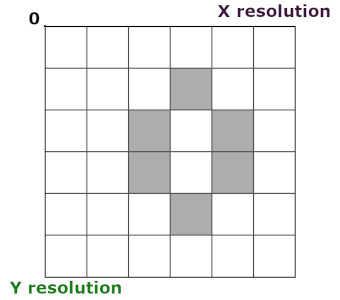
Для примера возьмём матрицу с низким разрешением:

Каждая клетка в ней будет принимать два значения – 0 и 1; соответственно – мёртвая и живая.
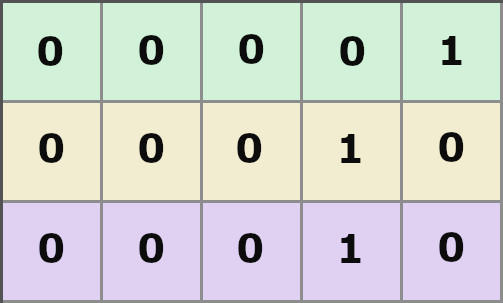
В этой матрице и будут выполняться все действия. Мы будем проходить последовательно по всем клеткам, слева направо и строка за строкой сверху вниз.
2. Проверяем окружение клетки
2.1 Осматриваем все соседние клетки
2.2 Подсчитываем количество живых соседей
Поскольку состояние клетки у нас может быть 1 или 0, просто складываем значения каждой соседней клетки, и их суммой будет количество живых соседей.
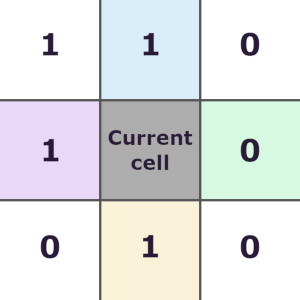
Для примера на картинке выше это будет: 1+1+0+0+0+1+0+1=4 (по часовой стрелке от левой верхней клетки).
3. Обрабатываем столкновения с краями матрицы
Поскольку матрица имеет конечные размеры, рано или поздно мы подойдём к её краям, и при проверке соседних клеток выйдем за её пределы. Чтобы избежать этого, надо случаи выхода за пределы матрицы обработать. Обычно делают так, чтобы нижняя граница была как бы продолжением верхней, а правая продолжением левой. И наоборот.
Скажем, если проверяемая нами клетка находится на нижней границе матрицы, то мы, проверяя её нижних соседей, смотрим на клетки, находящиеся над ней на верхней границе матрицы:

Подобным образом поступаем и на всех остальных границах:
4. Выполняем правила игры
Если живую клетку окружает менее 2-х или более 3-х живых, она умирает; если мёртвую клетку окружает ровно 3 живые, она оживает. В нашем случае текущую клетку окружает 4 живых соседа. Если бы это была живая клетка, она бы стала мёртвой, в противном случае ничего бы не произошло.
***
Вот и всё. Довольно простая штука. Остаётся только отрисовать матрицу, но это уже к механике игры не относится. Правда, в механике остался один момент, без которого игра нормально работать не будет – при обработке кадра результат действий нужно записывать в новую матрицу, копию той, которая получилась после обработки предыдущего кадра. Иначе игра будет работать неправильно. Впрочем, подробнее об этом и обо всём – ниже.
Теперь посмотрим на то, как игра «Жизнь» работает на Python и JavaScript.
Игра «Жизнь» на JavaScript(к содержанию ^)
Давайте взглянем на весь код:
Сразу после его запуска генерируется случайная матрица, после чего начинается игровой процесс. JS-версию можно запустить в браузере (для перезапуска игры нажмите «Сбросить»):
Нас будет интересовать преимущественно то, что происходит внутри функции drawCells(). Но для начала создадим матрицу – то есть сгенерируем двухмерный массив.
Создаём матрицу
Двухмерный массив сделаем этой строкой:
Значения переменных (точнее, констант) yRes и xRes задаются выше:
В итоге получившийся двухмерный массив cells будет содержать 20 одномерных массивов по 40 элементов в каждом. То есть мы получили матрицу разрешением в 20 строк по 40 клеток в каждой строке. Правда, сейчас все её элементы не определены – имеют значение undefined.
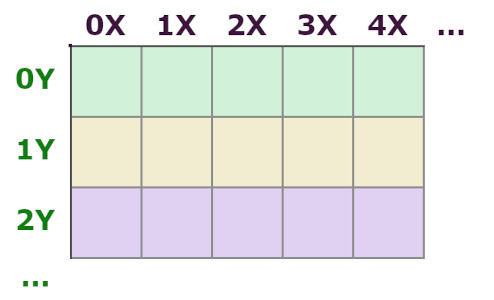
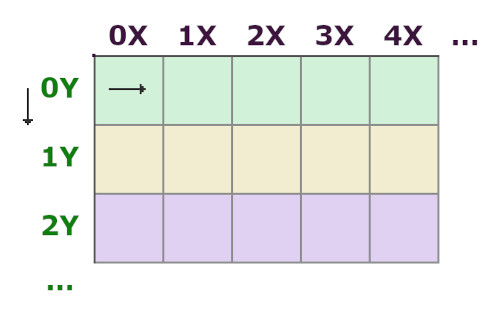
Количество строк отмечено по оси Y, а количество клеток в строках – по оси X.
Теперь остаётся поместить в ячейки нужные значения, 1 или 0. Это мы делаем пользовательской функцией getRandomMatrix(), генерирующей случайным образом единицу или ноль для каждой ячейки.
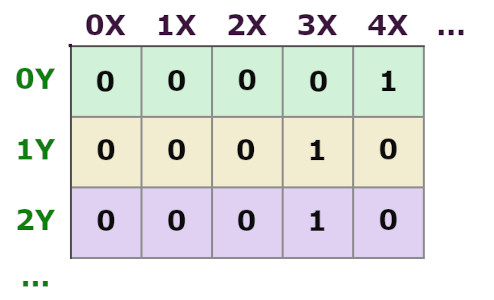
Всё готово! И напоследок обратим внимание на пару вещей:
> Почему на картинке нумерация X и Y начинается с 0?
В JavaScript элементы массива индексируются не с единицы, а с нуля. То есть в массиве из 3-х элементов они будут проиндексированы как 0,1,2, а не 1,2,3. Похожие вещи происходят и с другими языками программирования, в т.ч. и с Python.
> Почему номера (индексы) строк увеличиваются сверху вниз?
В canvas на html, как и в canvas Tkinter’а на Python значения по оси Y увеличиваются сверху вниз, а не снизу вверх:

Тогда как значения по оси X возрастают слева направо.
Проходим по клеткам матрицы
Один кадр анимации создаётся функцией drawCells(), тогда как за смену кадров и частоту их смены отвечает функция animate(). Её мы и вызываем после getRandomMatrix().
Внутри вложенного цикла for мы последовательно проверяем все элементы массива, то есть клетки матрицы.
Цикл for содержит 3 выражения:
1. Объявление переменной. Она создаётся один раз перед началом цикла будет видна только в его пределах;
2. Проверка условия выполнения перед каждой итерацией;
3. Код, выполняющийся в конце каждой итерации.
Первый for отвечает за перебор индексов строк матрицы (одномерных массивов). Мы объявляем переменную счётчика – let itrY = 0. Она будет увеличиваться на единицу каждую итерацию – itrY++. И каждый раз мы проверяем условие itrY < yRes – пока переменная itrY меньше yRes, разрешения матрицы по Y, цикл работает. Иначе он останавливается.
Второй цикл for выполняется каждую итерацию первого и отвечает за перебор клеток текущей строки (элементов текущего одномерного массива). Тут происходит то же самое – объявляется переменная счётчика let itrX = 0, увеличивается каждый раз на единицу itrX++ и проверяется, меньше ли она разрешения матрицы по X – itrX < xRes. Если нет, завершаем цикл и переходим к следующей строке (начинается следующая итерация первого цикла).
Происходит что-то вроде этого:
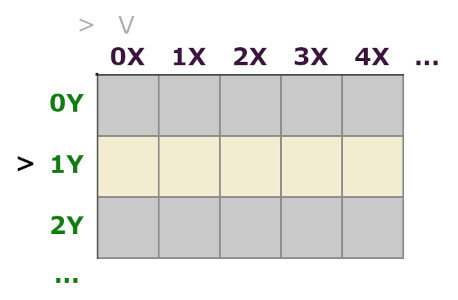
Мы перебираем строки от первой до последней, останавливаясь на каждой и перебирая в ней все клетки так же от первой до последней.
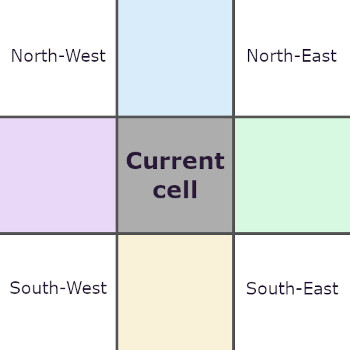
Определяем координаты соседей
Для начала нам понадобится определить соседние клетки по вертикали и горизонтали – сверху, снизу, справа и слева. Условно – север, юг, запад и восток.
Матрица, как сказано выше, у нас представляет собой двухмерный массив, который можно представить так:

Чтобы переместиться по оси Y на единицу вверх или вниз, нам нужно перейти на одномерный массив индексом выше или ниже, т.е. увеличить или уменьшить переменную, отвечающую за индекс текущего массива на 1. Чтобы переместиться на единицу по оси X мы должны, соответственно, увеличить или уменьшить индекс текущего элемента на 1.
Находим количество «живых» соседей
Для этого складываем значения из клеток вокруг текущей клетки.
Сделал складывание в две строки для наглядности, это можно сделать и одной строкой. Первой строкой складываются значения в клетках с «севера», «юга», «запада» и «востока». Например, cells[north][itrX] будет содержать элемент с текущим индексом, но из одномерного массива индексом выше. Первое значение в скобках [north] – индекс одномерного массива, второе [itrX] – индекс его элемента.
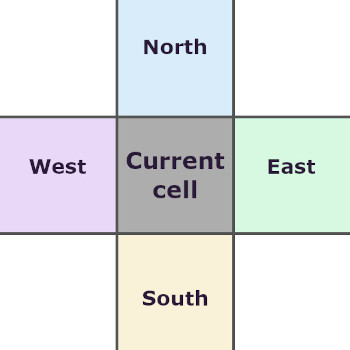
Второй строкой прибавляются значения в клетках по диагонали – «северо-запад», «северо-восток», «юго-запад» и «юго-восток». Например, в cells[north][east] мы переходим в массив выше (с индексом на 1 меньше) и на его элемент левее (с индексом на 1 больше).
Каждый элемент имеет значение 1 или 0, поэтому их сумма и будет количеством «живых» соседей.
Обрабатываем выход за матрицу
Сначала нужно учесть, что массивы индексируются не от единицы, а от нуля. Поэтому в массиве, где 40 элементов, индекс последнего – 39. Переменные yRes и xRes содержат количество их элементов, а чтобы узнать индекс последнего элемента, нужно отнять от этих переменных 1:
Затем делаем саму проверку:
Значения «north» и «west» могут стать только меньше 0. Если это так, они должны равняться соответственным максимальным индексам yResArr и xResArr.
Значения «south» и «east» могут стать только больше самых больших индексов. И если это так, они должны равняться 0.
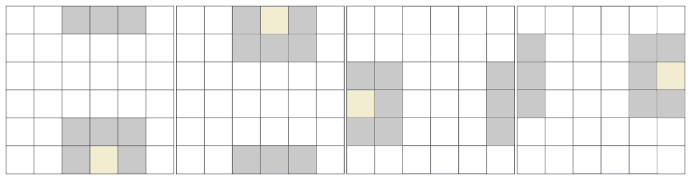
Таким образом любой край нашей матрицы будет как-бы продолжаться с противоположного края, и, для примера, одна из стабильных фигур, улей (hive), разделённая краем матрицы, будет выглядеть так:
В нормальном же виде он имеет такой вид:
Выполняем условия игры
Сначала проверяем, какое значение у клетки – 1 или 0. Если 0, смотрим, равно ли количество её соседей 3-м и, если да, устанавливаем значение 1. Иначе – проверяем, имеет ли клетка меньше 2-х или больше 3-х соседей. Если это так, устанавливаем значение 0.
Кое-что о массивах
На этом как бы всё заканчивается, остаётся только прорисовать матрицу. Но почему мы проверяем условие по массиву cells, а результаты записываем в newArray? Это и есть тот момент, без которого игра не будет работать нормально.
При обработке кадра проверку нужно делать по текущему массиву, а результат записывать в новый – копию текущего. Вначале функции drawCells(), перед вложенным циклом for, мы копируем массив cells в newArray:
Мы не можем скопировать массив, просто написав так:
В JavaScript, как и в Python, массивы – это объекты, а их имена – просто ссылки на них. И в данном случае у нас просто newArray и cells будут ссылаться на один и тот же массив. А чтобы его скопировать, в JS есть функция slice().
И вроде бы проблема решена, но есть нюанс – slice() работает только с одномерными массивами, а у нас он двухмерный. Если мы его попробуем скопировать этой функцией, у нас просто получится новый массив, содержащий ссылки на одномерные массивы старого.
Встроенной функции глубокого копирования в JavaScript нет, поэтому придётся написать свою, под наш случай:
Просто проходим циклом for по cells, последовательно копируя все одномерные массивы в newArray.
Прорисовка матрицы
Сначала в html создаём канвас (по простому – холст):
Он называется wnd и имеет разрешение 400 на 200. Затем в JavaScript нам нужно получить узел холста и присвоить ему контекст – первой и второй строкой соответственно:
В функции drawCells() внутри вложенного цикла for у нас есть эти две строки:
Для того, чтобы расположить прямоугольник в канвасе, нам нужно положение левого верхнего угла по координатам X (shiftX) и Y (shiftY). Поскольку мы будем рисовать квадраты, а все его стороны равны, поэтому для определения X и Y нам нужно соответствующие индексы умножить на сторону квадрата rSide.
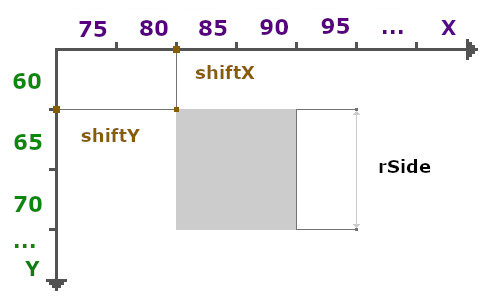
И если нам нужно нарисовать клетку из 6-го ряда в 8-й ячейке, то при стороне квадрата 10 пикселей X будет 8 * 10 = 80, а Y – 6 * 10 = 60.
И теперь рисуем саму клетку:
Делается это функцией fillRect(). Она принимает положение верхнего левого угла по X и Y, а также длину двух сторон. И поскольку мы рисуем квадрат, передаём просто одно и то же значение обеим сторонам.
fillStyle окрашивает прямоугольник в заданный цвет. Условие определяет, какое значение содержит клетка – 1 или 0. Если 1, рисуем одним цветом, иначе – другим.
Смена кадров
Для начала вычисляем время смены кадра и время загрузки страницы в миллисекундах:
В fpsLimit – количество кадров в секунду, а в interval вычисляется длительность каждого кадра делением 1000 мс (что есть одна секунда) на fpsLimit. В последней строке performance.now() возвращает время, прошедшее с загрузки страницы. То есть в lastTime мы записываем то количество миллисекунд, которое прошло после загрузки страницы перед запуском игрового процесса. Это будет время перед отрисовкой первого кадра.
Затем смену кадров выполняет функция animate():
Вместо цикла используется рекурсия – функция вызывает саму себя, в данном случае используя requestAnimationFrame(), метод браузера, контролирующий прорисовку анимаций. Каждый вызов функции мы определяем два значения – текущее время, прошедшее с начала загрузки страницы (now) и разницу между ним и временем отрисовки последнего кадра (deltaTime).
Затем проверяем, превысила ли deltaTime установленное время смены кадра (либо равна ему). Если да – время перед отрисовкой кадра становится текущее (lastTime = now). После этого вызываем отрисовку самого кадра, функцию drawCells().
***
Вот так работает игра «Жизнь» на JavaScript. А теперь давайте посмотрим, как можно сделать её на Python.
Игра «Жизнь» на Python(к содержанию ^)
Как и в JS-версии, сначала генерируется матрица, после чего запускается сам игровой процесс:
Создаём матрицу
На Python матрица будет представлять собой вложенный список (технически список в Python – массив). Сразу помещаем в её ячейки 0.
Сначала создаём список x_row, который будет представлять строки с клетками. Затем с помощью цикла for добавляем один за другим элементы с помощью метода append(). Этот метод добавляет элемент со значением в скобках (в нашем случае это 0) в конец списка.
Цикл for в нашем случае имеет два параметра – переменную счётчика i_xrow и то, до какого значения нужно продолжать выполнение. Это определяется функцией range(), создающей последовательность чисел и использующейся для ограничения количества итераций. Сейчас она создаёт последовательность от 0 до x_res-1 с шагом в единицу. Поэтому цикл будет срабатывать x_res раз; переменные x_res и y_res, отвечающие за разрешение матрицы по осям X и Y мы объявили в начале кода:
Похожим образом работает и второй цикл, но тут мы создаём вложенный список, добавляя каждый раз в конец копию x_row. Это делается функцией copy из модуля copy.
В Python имена списков (как и переменных, кортежей, словарей и т.д.) – просто ссылки на объекты, и, сделав что-то вроде a = b, a и b будут просто ссылаться на один и тот же объект. Поэтому мы и пользуемся копированием.
Матрица в виде вложенного списка y_res из обычных списков по x_res элементов готова. Теперь просто обрабатываем её пользовательской функцией matrix_rand(), которая генерирует случайную конфигурацию значений её элементов.
Перебираем кадры и клетки матрицы
Чередование кадров происходит в бесконечном цикле while:
Первый цикл чередует строки, т.е. обычные списки, а второй – элементы каждого. Каждую итерацию в переменных iy_row и ix_row будут индексы текущего списка и текущего элемента в нём соответственно.
Определяем соседей и подсчитываем их
Как и в JS-версии, нам нужно определить стороны по вертикали и горизонтали. Условно – «север», «юг», «запад» и «восток».
За «север» и «юг» отвечает iy_row. Поэтому нам нужно либо отнять у неё единицу, либо прибавить. За «запад» и «восток» отвечает ix_row. Поэтому нам нужно также либо отнять у неё единицу, либо прибавить.
Теперь можно подсчитать количество «живых» соседей:
В первой строке подсчитываем соседей сверху, снизу, слева и справа.
Поскольку клетка (т.е. элемент списка) содержит либо 0, либо 1, подсчитать количество единиц можно просто сложив значения всех соседей. Для того, чтобы попасть на соседа сверху, нужно остаться на том же месте по координате X, но подняться на 1 по Y – y_row[north][ix_row]. Первый индекс нашего вложенного списка отвечает за обычный список, а второй за его элемент.

Таким же образом определяем остальные стороны.
Во второй строке определяем соседей по диагонали. Например, чтобы определить соседа на «северо-востоке», нам нужно сначала сместиться на одну клетку вверх, а затем на одну вправо – y_row[north][east]. То есть сначала на «север», затем на «восток». По такому же принципу определяем и остальных.

В итоге сумма всех соседних клеток и будет количеством «живых» соседей.
Предусматриваем столкновения с краями
Для этого сделаем так, чтобы левая сторона была как бы продолжением правой, верхняя продолжением нижней, и наоборот.
Стать меньше нуля могут только северная и южная стороны. Поэтому если это так, они равны максимальному разрешению по Y и X. Больше максимального разрешения матрицы по Y и X могут стать только южная и восточная стороны. И если это так, они равны 0.
И в случаях выхода за границы осмотр клеток выглядит так:

Текущая клетка выделена жёлтым, соседние – серым.
Проверяем условия игры
Сначала смотрим значение текущей клетки – 1 или 0. Если 0, проверяем, чтобы количество «живых» соседей было ровно 3 и, если это так, присваиваем значение 1. Если значение текущей клетки 0, смотрим, меньше ли двух или больше трёх «живых» соседей она имеет, и, если да – присваиваем значение 0.
Про копию списка
При обработке кадра сверять данные мы должны с текущим списком, а результаты записывать в его копию. Поэтому проверку мы делаем в y_row, а изменения вносим в new_row.
Копию этого списка нужно сделать перед началом обработки текущего кадра, перед вложенным циклом for:
Нужно использовать глубокое копирование – метод deepcopy(). В Python он находится в модуле copy. После обработки кадра, то есть после вложенного цикла for, мы присваиваем эту копию y_row:
Правильная работа игры
В итоге всё будет работать таким образом:

(нажмите чтобы увидеть анимацию)
«Неправильная» работа игры
А что, если записывать результаты в тот же список, с которым и сверяем? Стабильные фигуры работают как обычно. А вот движущиеся, вроде глайдера, ведут себя странно:
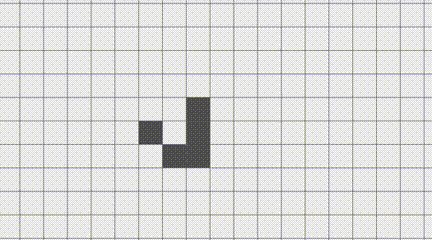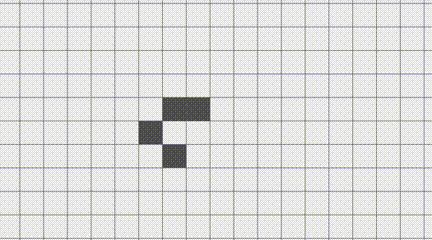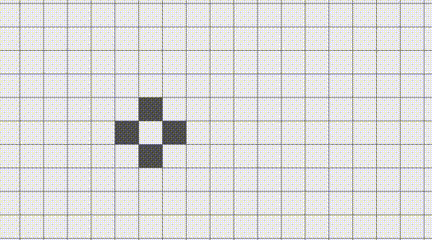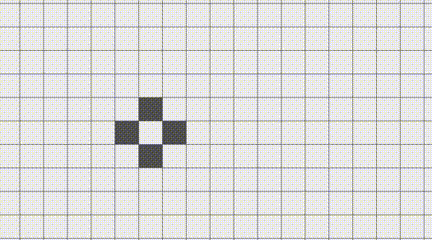
(нажмите чтобы увидеть анимацию*)
Если просто сгенерировать случайную конфигурацию клеток, колония растёт:

(нажмите чтобы увидеть анимацию*)
Тогда как в нормальном случае чаще всего происходит наоборот.
Прорисовываем кадры в Tkinter
Первой строкой создаём окно, второй называем его «Game of Life», третьей устанавливаем разрешение окна переменной win_res. Вообще, можно было бы просто задать его строкой, скажем, «800x800». Но можно сделать поинтересней:
Это называется f-строка, и она позволяет использовать переменные в строках. Для этого нужно использовать фигурные скобки {}.
В нашем случае мы вычисляем размеры окна по высоте и ширине умножая x_res или y_res, количество клеток в матрице по ширине и высоте, на сторону квадрата rect_side. Затем добавляем 3 пикселя просто для создания отступа – этого можно и не делать.
Создаём канвас, и с помощью менеджера pack() задаём ему два параметра – fill и expand:
> expand=True (или можно написать expand=1) выделяет под виджет всё доступное в окне пространство;
> fill=BOTH заполняет виджетом всё доступное пространство по ширине и высоте. Если написать fill=X, виджет заполнит пространство только по ширине, а в случае fill=Y – по высоте.
Внутри вложенного цикла for находим координаты квадрата, которым обозначается текущая обрабатываемая клетка:
Для того, чтобы нарисовать прямоугольник (или, в нашем случае, квадрат) в Tkinter, нам нужно знать координаты верхнего левого и нижнего правого углов. Сначала вычисляем координаты верхнего левого угла shift_x и shift_y, умножая координаты текущей клетки в матрице на длину стороны квадрата rect_side, затем координаты нижнего правого end_x и end_y, прибавляя к ним эту же сторону квадрата rect_side.
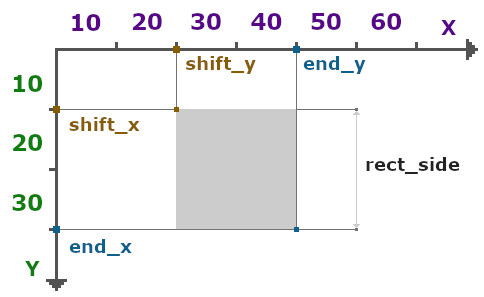
В системе координат канваса Tkinter’а значения по оси Y при движении вниз возрастают:

И теперь можно нарисовать текущую клетку в виде квадрата:
Создаём переменную board_color с нужным нам цветом, и затем, если текущая клетка имеет значение 1, задаём этой переменной другой цвет. С помощью create_rectangle() создаём прямоугольник. Первые два параметра – координаты левого верхнего угла по ширине и высоте, вторые два – координаты правого нижнего угла по ширине и высоте. Параметр fill задаёт цвет заливки, а outline – цвет обводки.
В конце цикла while делаем такие действия:
В time.sleep() задаём время паузы цикла, затем обновляем окно и очищаем его.
Последняя строка screen.mainloop() – бесконечный цикл созданного нами окна в Tkinter. В нём обрабатывается всё, что связано с созданным нами окном.
Итог
На этом и остановимся. Из простых вещей, буквально из двух-трёх правил, могут получаться действительно интересные штуки вроде игры «Жизнь».
Всем спасибо за внимание
P.S. Особое спасибо aNNiMON'у за помощь
______
* для мобильной версии
Игра «Жизнь» (Game of Life) придумана Джоном Конвеем в 1970-м году. Это – игра без игроков. Клеточный автомат, имитирующий жизнь колонии неких существ: прямоугольная площадка поделена на клетки, условно их представляющих. Правила просты, но игра интересная. Тут возможны, скажем, такие фигуры:

(нажмите чтобы увидеть анимацию*)Клетка может быть живой или мёртвой. Чем это определяется?
1. Если живую клетку окружает менее 2-х или более 3-х живых соседей, она погибает;
2. Если мёртвую клетку окружает ровно 3 живых соседа, она оживает.
Сделаем свою игру «Жизнь»? Что ж, приступим.
Содержание1. Как работает механика игры
2. Игра «Жизнь» на JavaScript
3. Игра «Жизнь» на Python
Как работает механика игры
Мы должны следовать таким пунктам:
1. Создаём матрицу
Для примера возьмём матрицу с низким разрешением:

Каждая клетка в ней будет принимать два значения – 0 и 1; соответственно – мёртвая и живая.

В этой матрице и будут выполняться все действия. Мы будем проходить последовательно по всем клеткам, слева направо и строка за строкой сверху вниз.

2. Проверяем окружение клетки
2.1 Осматриваем все соседние клетки
2.2 Подсчитываем количество живых соседей
Поскольку состояние клетки у нас может быть 1 или 0, просто складываем значения каждой соседней клетки, и их суммой будет количество живых соседей.

Для примера на картинке выше это будет: 1+1+0+0+0+1+0+1=4 (по часовой стрелке от левой верхней клетки).
3. Обрабатываем столкновения с краями матрицы
Поскольку матрица имеет конечные размеры, рано или поздно мы подойдём к её краям, и при проверке соседних клеток выйдем за её пределы. Чтобы избежать этого, надо случаи выхода за пределы матрицы обработать. Обычно делают так, чтобы нижняя граница была как бы продолжением верхней, а правая продолжением левой. И наоборот.
Скажем, если проверяемая нами клетка находится на нижней границе матрицы, то мы, проверяя её нижних соседей, смотрим на клетки, находящиеся над ней на верхней границе матрицы:

Подобным образом поступаем и на всех остальных границах:

4. Выполняем правила игры
Если живую клетку окружает менее 2-х или более 3-х живых, она умирает; если мёртвую клетку окружает ровно 3 живые, она оживает. В нашем случае текущую клетку окружает 4 живых соседа. Если бы это была живая клетка, она бы стала мёртвой, в противном случае ничего бы не произошло.
***
Вот и всё. Довольно простая штука. Остаётся только отрисовать матрицу, но это уже к механике игры не относится. Правда, в механике остался один момент, без которого игра нормально работать не будет – при обработке кадра результат действий нужно записывать в новую матрицу, копию той, которая получилась после обработки предыдущего кадра. Иначе игра будет работать неправильно. Впрочем, подробнее об этом и обо всём – ниже.
Теперь посмотрим на то, как игра «Жизнь» работает на Python и JavaScript.
Игра «Жизнь» на JavaScript(к содержанию ^)
Давайте взглянем на весь код:
Открыть спойлер
Сразу после его запуска генерируется случайная матрица, после чего начинается игровой процесс. JS-версию можно запустить в браузере (для перезапуска игры нажмите «Сбросить»):
Нас будет интересовать преимущественно то, что происходит внутри функции drawCells(). Но для начала создадим матрицу – то есть сгенерируем двухмерный массив.
Создаём матрицу
Двухмерный массив сделаем этой строкой:
- let cells = Array.from(Array(yRes), () => new Array(xRes))
Значения переменных (точнее, констант) yRes и xRes задаются выше:
- const xRes = 40;
- const yRes = 20;
В итоге получившийся двухмерный массив cells будет содержать 20 одномерных массивов по 40 элементов в каждом. То есть мы получили матрицу разрешением в 20 строк по 40 клеток в каждой строке. Правда, сейчас все её элементы не определены – имеют значение undefined.

Количество строк отмечено по оси Y, а количество клеток в строках – по оси X.
Теперь остаётся поместить в ячейки нужные значения, 1 или 0. Это мы делаем пользовательской функцией getRandomMatrix(), генерирующей случайным образом единицу или ноль для каждой ячейки.

Всё готово! И напоследок обратим внимание на пару вещей:
> Почему на картинке нумерация X и Y начинается с 0?
В JavaScript элементы массива индексируются не с единицы, а с нуля. То есть в массиве из 3-х элементов они будут проиндексированы как 0,1,2, а не 1,2,3. Похожие вещи происходят и с другими языками программирования, в т.ч. и с Python.
> Почему номера (индексы) строк увеличиваются сверху вниз?
В canvas на html, как и в canvas Tkinter’а на Python значения по оси Y увеличиваются сверху вниз, а не снизу вверх:

Тогда как значения по оси X возрастают слева направо.
Проходим по клеткам матрицы
Один кадр анимации создаётся функцией drawCells(), тогда как за смену кадров и частоту их смены отвечает функция animate(). Её мы и вызываем после getRandomMatrix().
Внутри вложенного цикла for мы последовательно проверяем все элементы массива, то есть клетки матрицы.
- for (let itrY = 0; itrY < yRes; itrY++) {
- for (let itrX = 0; itrX < xRes; itrX++) {
- …
- }
- }
Цикл for содержит 3 выражения:
1. Объявление переменной. Она создаётся один раз перед началом цикла будет видна только в его пределах;
2. Проверка условия выполнения перед каждой итерацией;
3. Код, выполняющийся в конце каждой итерации.
Первый for отвечает за перебор индексов строк матрицы (одномерных массивов). Мы объявляем переменную счётчика – let itrY = 0. Она будет увеличиваться на единицу каждую итерацию – itrY++. И каждый раз мы проверяем условие itrY < yRes – пока переменная itrY меньше yRes, разрешения матрицы по Y, цикл работает. Иначе он останавливается.
Второй цикл for выполняется каждую итерацию первого и отвечает за перебор клеток текущей строки (элементов текущего одномерного массива). Тут происходит то же самое – объявляется переменная счётчика let itrX = 0, увеличивается каждый раз на единицу itrX++ и проверяется, меньше ли она разрешения матрицы по X – itrX < xRes. Если нет, завершаем цикл и переходим к следующей строке (начинается следующая итерация первого цикла).
Происходит что-то вроде этого:

Мы перебираем строки от первой до последней, останавливаясь на каждой и перебирая в ней все клетки так же от первой до последней.
Определяем координаты соседей
Для начала нам понадобится определить соседние клетки по вертикали и горизонтали – сверху, снизу, справа и слева. Условно – север, юг, запад и восток.
- let north = itrY - 1;
- let south = itrY + 1;
- let west = itrX - 1;
- let east = itrX + 1;
Матрица, как сказано выше, у нас представляет собой двухмерный массив, который можно представить так:

Чтобы переместиться по оси Y на единицу вверх или вниз, нам нужно перейти на одномерный массив индексом выше или ниже, т.е. увеличить или уменьшить переменную, отвечающую за индекс текущего массива на 1. Чтобы переместиться на единицу по оси X мы должны, соответственно, увеличить или уменьшить индекс текущего элемента на 1.
Находим количество «живых» соседей
Для этого складываем значения из клеток вокруг текущей клетки.
- let nb = 0;
- nb = cells[north][itrX] + cells[south][itrX] + cells[itrY][west] + cells[itrY][east];
- nb = nb + cells[north][west] + cells[north][east] + cells[south][west] + cells[south][east];
Сделал складывание в две строки для наглядности, это можно сделать и одной строкой. Первой строкой складываются значения в клетках с «севера», «юга», «запада» и «востока». Например, cells[north][itrX] будет содержать элемент с текущим индексом, но из одномерного массива индексом выше. Первое значение в скобках [north] – индекс одномерного массива, второе [itrX] – индекс его элемента.

Второй строкой прибавляются значения в клетках по диагонали – «северо-запад», «северо-восток», «юго-запад» и «юго-восток». Например, в cells[north][east] мы переходим в массив выше (с индексом на 1 меньше) и на его элемент левее (с индексом на 1 больше).

Каждый элемент имеет значение 1 или 0, поэтому их сумма и будет количеством «живых» соседей.
Обрабатываем выход за матрицу
Сначала нужно учесть, что массивы индексируются не от единицы, а от нуля. Поэтому в массиве, где 40 элементов, индекс последнего – 39. Переменные yRes и xRes содержат количество их элементов, а чтобы узнать индекс последнего элемента, нужно отнять от этих переменных 1:
- let yResArr = yRes - 1;
- let xResArr = xRes - 1;
Затем делаем саму проверку:
- if (north < 0) {
- north = yResArr;
- }
- if (south > yResArr) {
- south = 0;
- }
- if (west < 0) {
- west = xResArr;
- }
- if (east > xResArr) {
- east = 0;
- }
Значения «north» и «west» могут стать только меньше 0. Если это так, они должны равняться соответственным максимальным индексам yResArr и xResArr.
Значения «south» и «east» могут стать только больше самых больших индексов. И если это так, они должны равняться 0.
Таким образом любой край нашей матрицы будет как-бы продолжаться с противоположного края, и, для примера, одна из стабильных фигур, улей (hive), разделённая краем матрицы, будет выглядеть так:

В нормальном же виде он имеет такой вид:

Выполняем условия игры
- if (cells[itrY][itrX] == 0) {
- if (nb == 3) {
- newArray[itrY][itrX] = 1;
- }
- } else {
- if (nb < 2 || nb > 3) {
- newArray[itrY][itrX] = 0;
- }
- }
Сначала проверяем, какое значение у клетки – 1 или 0. Если 0, смотрим, равно ли количество её соседей 3-м и, если да, устанавливаем значение 1. Иначе – проверяем, имеет ли клетка меньше 2-х или больше 3-х соседей. Если это так, устанавливаем значение 0.
Кое-что о массивах
На этом как бы всё заканчивается, остаётся только прорисовать матрицу. Но почему мы проверяем условие по массиву cells, а результаты записываем в newArray? Это и есть тот момент, без которого игра не будет работать нормально.
При обработке кадра проверку нужно делать по текущему массиву, а результат записывать в новый – копию текущего. Вначале функции drawCells(), перед вложенным циклом for, мы копируем массив cells в newArray:
- let newArray = deepCopy(cells, yRes);
Мы не можем скопировать массив, просто написав так:
- let newArray = cells;
В JavaScript, как и в Python, массивы – это объекты, а их имена – просто ссылки на них. И в данном случае у нас просто newArray и cells будут ссылаться на один и тот же массив. А чтобы его скопировать, в JS есть функция slice().
И вроде бы проблема решена, но есть нюанс – slice() работает только с одномерными массивами, а у нас он двухмерный. Если мы его попробуем скопировать этой функцией, у нас просто получится новый массив, содержащий ссылки на одномерные массивы старого.
Встроенной функции глубокого копирования в JavaScript нет, поэтому придётся написать свою, под наш случай:
- function deepCopy(cells, yRes) {
- let newArray = [];
- for (let i = 0; i < yRes; i++) {
- newArray.push(cells[i].slice());
- }
- return newArray
- }
Просто проходим циклом for по cells, последовательно копируя все одномерные массивы в newArray.
Прорисовка матрицы
Сначала в html создаём канвас (по простому – холст):
- <canvas id="wnd" width="400" height="200"></canvas>
Он называется wnd и имеет разрешение 400 на 200. Затем в JavaScript нам нужно получить узел холста и присвоить ему контекст – первой и второй строкой соответственно:
- const canvas = document.getElementById("wnd");
- const ctx = canvas.getContext("2d");
В функции drawCells() внутри вложенного цикла for у нас есть эти две строки:
- let shiftX = itrX * rSide;
- let shiftY = itrY * rSide;
Для того, чтобы расположить прямоугольник в канвасе, нам нужно положение левого верхнего угла по координатам X (shiftX) и Y (shiftY). Поскольку мы будем рисовать квадраты, а все его стороны равны, поэтому для определения X и Y нам нужно соответствующие индексы умножить на сторону квадрата rSide.

И если нам нужно нарисовать клетку из 6-го ряда в 8-й ячейке, то при стороне квадрата 10 пикселей X будет 8 * 10 = 80, а Y – 6 * 10 = 60.
И теперь рисуем саму клетку:
- if (cells[itrY][itrX] == 1) {
- ctx.fillStyle = "#dfdfdf";
- } else {
- ctx.fillStyle = "#969696";
- }
- ctx.fillRect(shiftX, shiftY, rSide, rSide);
Делается это функцией fillRect(). Она принимает положение верхнего левого угла по X и Y, а также длину двух сторон. И поскольку мы рисуем квадрат, передаём просто одно и то же значение обеим сторонам.
fillStyle окрашивает прямоугольник в заданный цвет. Условие определяет, какое значение содержит клетка – 1 или 0. Если 1, рисуем одним цветом, иначе – другим.
Смена кадров
Для начала вычисляем время смены кадра и время загрузки страницы в миллисекундах:
- const fpsLimit = 20;
- const interval = 1000.0 / fpsLimit;
- let lastTime = performance.now();
В fpsLimit – количество кадров в секунду, а в interval вычисляется длительность каждого кадра делением 1000 мс (что есть одна секунда) на fpsLimit. В последней строке performance.now() возвращает время, прошедшее с загрузки страницы. То есть в lastTime мы записываем то количество миллисекунд, которое прошло после загрузки страницы перед запуском игрового процесса. Это будет время перед отрисовкой первого кадра.
Затем смену кадров выполняет функция animate():
- function animate() {
- const now = performance.now();
- const deltaTime = now - lastTime;
- if (deltaTime >= interval) {
- lastTime = now;
- drawCells();
- }
- requestAnimationFrame(animate);
- }
Вместо цикла используется рекурсия – функция вызывает саму себя, в данном случае используя requestAnimationFrame(), метод браузера, контролирующий прорисовку анимаций. Каждый вызов функции мы определяем два значения – текущее время, прошедшее с начала загрузки страницы (now) и разницу между ним и временем отрисовки последнего кадра (deltaTime).
Затем проверяем, превысила ли deltaTime установленное время смены кадра (либо равна ему). Если да – время перед отрисовкой кадра становится текущее (lastTime = now). После этого вызываем отрисовку самого кадра, функцию drawCells().
***
Вот так работает игра «Жизнь» на JavaScript. А теперь давайте посмотрим, как можно сделать её на Python.
Игра «Жизнь» на Python(к содержанию ^)
Как и в JS-версии, сначала генерируется матрица, после чего запускается сам игровой процесс:
Открыть спойлер
Создаём матрицу
На Python матрица будет представлять собой вложенный список (технически список в Python – массив). Сразу помещаем в её ячейки 0.
- x_row: list = []
- for i_xrow in range(x_res):
- x_row.append(0)
- y_row: list = []
- for i_yrow in range(y_res):
- y_row.append(copy.copy(x_row))
Сначала создаём список x_row, который будет представлять строки с клетками. Затем с помощью цикла for добавляем один за другим элементы с помощью метода append(). Этот метод добавляет элемент со значением в скобках (в нашем случае это 0) в конец списка.
Цикл for в нашем случае имеет два параметра – переменную счётчика i_xrow и то, до какого значения нужно продолжать выполнение. Это определяется функцией range(), создающей последовательность чисел и использующейся для ограничения количества итераций. Сейчас она создаёт последовательность от 0 до x_res-1 с шагом в единицу. Поэтому цикл будет срабатывать x_res раз; переменные x_res и y_res, отвечающие за разрешение матрицы по осям X и Y мы объявили в начале кода:
- x_res: int = 32
- y_res: int = 18
Похожим образом работает и второй цикл, но тут мы создаём вложенный список, добавляя каждый раз в конец копию x_row. Это делается функцией copy из модуля copy.
В Python имена списков (как и переменных, кортежей, словарей и т.д.) – просто ссылки на объекты, и, сделав что-то вроде a = b, a и b будут просто ссылаться на один и тот же объект. Поэтому мы и пользуемся копированием.
Матрица в виде вложенного списка y_res из обычных списков по x_res элементов готова. Теперь просто обрабатываем её пользовательской функцией matrix_rand(), которая генерирует случайную конфигурацию значений её элементов.
Перебираем кадры и клетки матрицы
Чередование кадров происходит в бесконечном цикле while:
- while True:
- …
- Пока True равно True всё будет работать.
- Обработка каждой клетки матрицы происходит внутри вложенного цикла for:
- for iy_row in range(y_res):
- for ix_row in range(x_res):
- …
Первый цикл чередует строки, т.е. обычные списки, а второй – элементы каждого. Каждую итерацию в переменных iy_row и ix_row будут индексы текущего списка и текущего элемента в нём соответственно.
Определяем соседей и подсчитываем их
Как и в JS-версии, нам нужно определить стороны по вертикали и горизонтали. Условно – «север», «юг», «запад» и «восток».
- north: int = iy_row - 1
- south: int = iy_row + 1
- west: int = ix_row - 1
- east: int = ix_row + 1
За «север» и «юг» отвечает iy_row. Поэтому нам нужно либо отнять у неё единицу, либо прибавить. За «запад» и «восток» отвечает ix_row. Поэтому нам нужно также либо отнять у неё единицу, либо прибавить.
Теперь можно подсчитать количество «живых» соседей:
- nb: int = y_row[north][ix_row] + y_row[south][ix_row] + y_row[iy_row][west] + y_row[iy_row][east]
- nb = nb + y_row[north][west] + y_row[north][east] + y_row[south][west] + y_row[south][east]
В первой строке подсчитываем соседей сверху, снизу, слева и справа.
Поскольку клетка (т.е. элемент списка) содержит либо 0, либо 1, подсчитать количество единиц можно просто сложив значения всех соседей. Для того, чтобы попасть на соседа сверху, нужно остаться на том же месте по координате X, но подняться на 1 по Y – y_row[north][ix_row]. Первый индекс нашего вложенного списка отвечает за обычный список, а второй за его элемент.

Таким же образом определяем остальные стороны.
Во второй строке определяем соседей по диагонали. Например, чтобы определить соседа на «северо-востоке», нам нужно сначала сместиться на одну клетку вверх, а затем на одну вправо – y_row[north][east]. То есть сначала на «север», затем на «восток». По такому же принципу определяем и остальных.

В итоге сумма всех соседних клеток и будет количеством «живых» соседей.
Предусматриваем столкновения с краями
Для этого сделаем так, чтобы левая сторона была как бы продолжением правой, верхняя продолжением нижней, и наоборот.
- if north < 0:
- north = y_list
- if south > y_list:
- south = 0
- if west < 0:
- west = x_list
- if east > x_list:
- east = 0
Стать меньше нуля могут только северная и южная стороны. Поэтому если это так, они равны максимальному разрешению по Y и X. Больше максимального разрешения матрицы по Y и X могут стать только южная и восточная стороны. И если это так, они равны 0.
И в случаях выхода за границы осмотр клеток выглядит так:

Текущая клетка выделена жёлтым, соседние – серым.
Проверяем условия игры
- if y_row[iy_row][ix_row] == 0:
- if nb == 3:
- new_row[iy_row][ix_row] = 1
- else:
- if nb < 2 or nb > 3:
- new_row[iy_row][ix_row] = 0
Сначала смотрим значение текущей клетки – 1 или 0. Если 0, проверяем, чтобы количество «живых» соседей было ровно 3 и, если это так, присваиваем значение 1. Если значение текущей клетки 0, смотрим, меньше ли двух или больше трёх «живых» соседей она имеет, и, если да – присваиваем значение 0.
Про копию списка
При обработке кадра сверять данные мы должны с текущим списком, а результаты записывать в его копию. Поэтому проверку мы делаем в y_row, а изменения вносим в new_row.
Копию этого списка нужно сделать перед началом обработки текущего кадра, перед вложенным циклом for:
- new_row = copy.deepcopy(y_row)
Нужно использовать глубокое копирование – метод deepcopy(). В Python он находится в модуле copy. После обработки кадра, то есть после вложенного цикла for, мы присваиваем эту копию y_row:
- y_row = new_row
Правильная работа игры
В итоге всё будет работать таким образом:

(нажмите чтобы увидеть анимацию)
«Неправильная» работа игры
А что, если записывать результаты в тот же список, с которым и сверяем? Стабильные фигуры работают как обычно. А вот движущиеся, вроде глайдера, ведут себя странно:
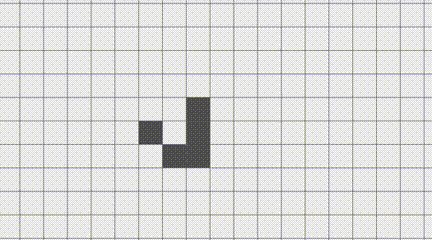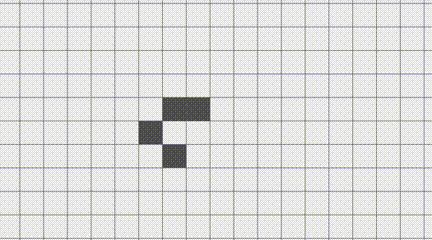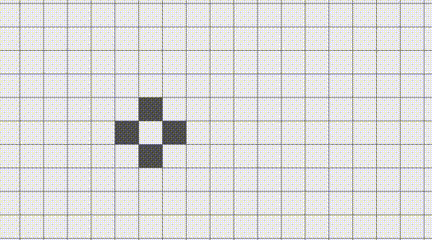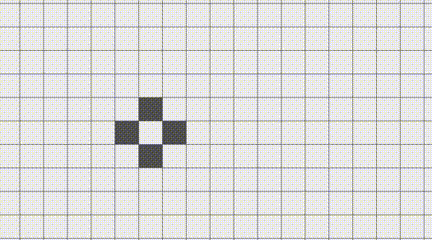
(нажмите чтобы увидеть анимацию*)
Если просто сгенерировать случайную конфигурацию клеток, колония растёт:

(нажмите чтобы увидеть анимацию*)
Тогда как в нормальном случае чаще всего происходит наоборот.
Прорисовываем кадры в Tkinter
- screen = Tk()
- screen.title('Game of Life')
- screen.geometry(win_res)
- board = Canvas(screen)
- board.pack(fill=BOTH, expand=True)
Первой строкой создаём окно, второй называем его «Game of Life», третьей устанавливаем разрешение окна переменной win_res. Вообще, можно было бы просто задать его строкой, скажем, «800x800». Но можно сделать поинтересней:
- win_res: str = f"{x_res * rect_side + 3}x{y_res * rect_side + 3}"
Это называется f-строка, и она позволяет использовать переменные в строках. Для этого нужно использовать фигурные скобки {}.
В нашем случае мы вычисляем размеры окна по высоте и ширине умножая x_res или y_res, количество клеток в матрице по ширине и высоте, на сторону квадрата rect_side. Затем добавляем 3 пикселя просто для создания отступа – этого можно и не делать.
Создаём канвас, и с помощью менеджера pack() задаём ему два параметра – fill и expand:
> expand=True (или можно написать expand=1) выделяет под виджет всё доступное в окне пространство;
> fill=BOTH заполняет виджетом всё доступное пространство по ширине и высоте. Если написать fill=X, виджет заполнит пространство только по ширине, а в случае fill=Y – по высоте.
Внутри вложенного цикла for находим координаты квадрата, которым обозначается текущая обрабатываемая клетка:
- shift_x: int = ix_row * rect_side
- shift_y: int = iy_row * rect_side
- end_x: int = shift_x + rect_side
- end_y: int = shift_y + rect_side
Для того, чтобы нарисовать прямоугольник (или, в нашем случае, квадрат) в Tkinter, нам нужно знать координаты верхнего левого и нижнего правого углов. Сначала вычисляем координаты верхнего левого угла shift_x и shift_y, умножая координаты текущей клетки в матрице на длину стороны квадрата rect_side, затем координаты нижнего правого end_x и end_y, прибавляя к ним эту же сторону квадрата rect_side.

В системе координат канваса Tkinter’а значения по оси Y при движении вниз возрастают:

И теперь можно нарисовать текущую клетку в виде квадрата:
- board_color = 'White'
- if y_row[iy_row][ix_row] == 1:
- board_color = '#494949'
- board.create_rectangle(shift_x, shift_y, end_x, end_y,
- fill=board_color, outline='#535353')
Создаём переменную board_color с нужным нам цветом, и затем, если текущая клетка имеет значение 1, задаём этой переменной другой цвет. С помощью create_rectangle() создаём прямоугольник. Первые два параметра – координаты левого верхнего угла по ширине и высоте, вторые два – координаты правого нижнего угла по ширине и высоте. Параметр fill задаёт цвет заливки, а outline – цвет обводки.
В конце цикла while делаем такие действия:
- time.sleep(sleep)
- screen.update()
- board.delete('all')
В time.sleep() задаём время паузы цикла, затем обновляем окно и очищаем его.
Последняя строка screen.mainloop() – бесконечный цикл созданного нами окна в Tkinter. В нём обрабатывается всё, что связано с созданным нами окном.
- screen.mainloop()
Итог
На этом и остановимся. Из простых вещей, буквально из двух-трёх правил, могут получаться действительно интересные штуки вроде игры «Жизнь».
Всем спасибо за внимание

P.S. Особое спасибо aNNiMON'у за помощь

______
* для мобильной версии


